Objective

Design a robust nonlinear path following control law for a fixed-wing UAV to track a reference path under the wind disturbance

 

Disturbance Observer

System model for the wind estimator

$$ \begin{bmatrix} \dot{x} \\ \dot{y} \end{bmatrix} = \begin{bmatrix} V_a \cos \psi + W_N \\ V_a \sin \psi + W_E \end{bmatrix}$$

Update law of the disturbance observer

$$ \dot{\hat{\bf{w}}} = -T_w \hat{\bf{w}} + T_w ( \dot{\bf{x}} – \bf{u}) $$
where, \( \hat{\bf{w}} = \begin{bmatrix} \hat W_n & \hat W_e \end{bmatrix}^T \) is the wind velocity estimate in the north and east direction, \( T_w \) is the diagonal observer gain matrix, and \( \bf{u} = \begin{bmatrix} V_a \cos \psi & V_a \sin \psi \end{bmatrix}^T \)

 

System Model

 

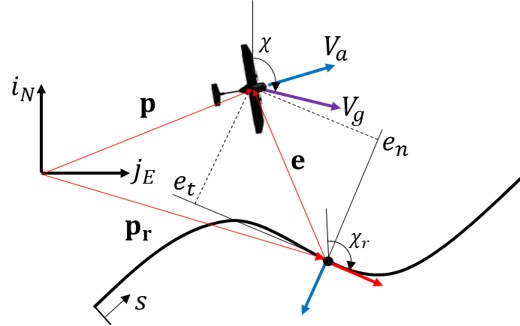
The error kinematics model becomes,

$$ \begin{align} \dot{e}_t &= V_g \cos (\chi – \chi_r ) – ( 1 – \kappa (s) e_n ) \dot{s} \\ \dot{e}_n &= V_g \sin (\chi – \chi_r ) – \kappa (s) e_t \dot{s} \end{align} $$

 

Path Following Control Law

Command Filtered Backstepping

 

 

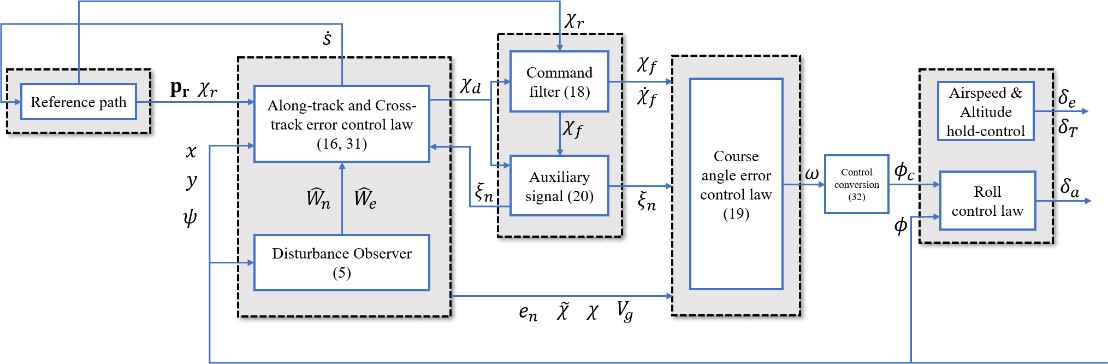
Hardware-in-the-loop Tests

Bspline Path Following

 

 

 

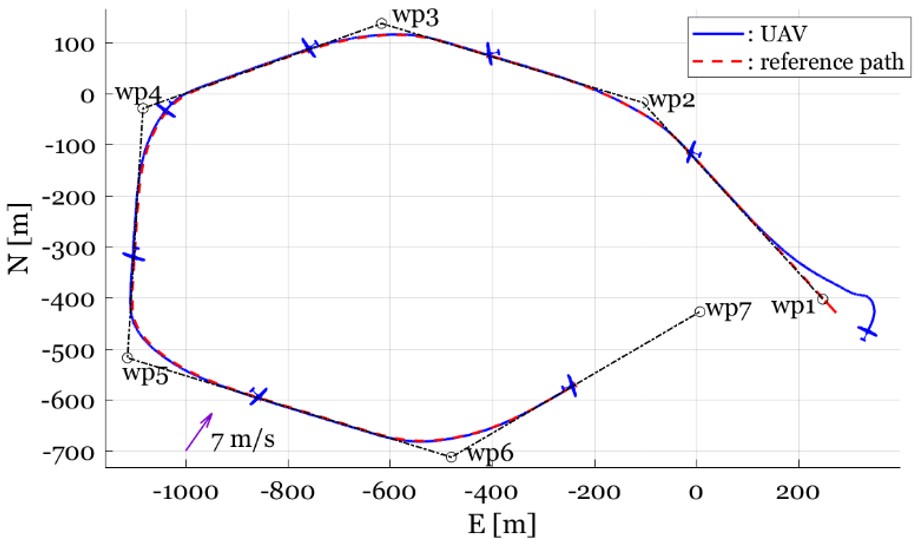
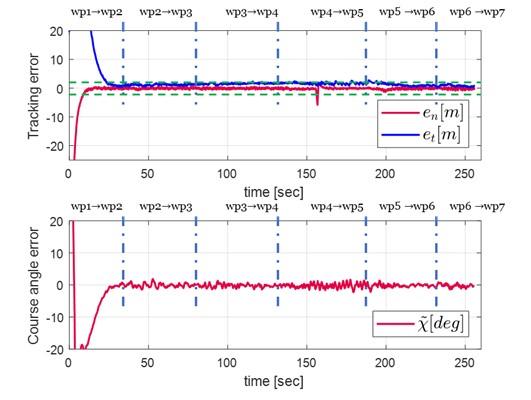
Flight Tests

Circular trajectory following

 

 

 

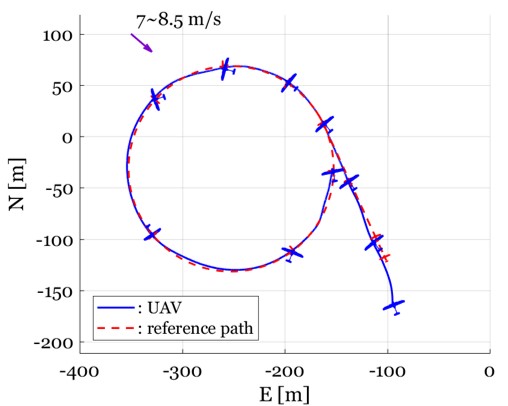
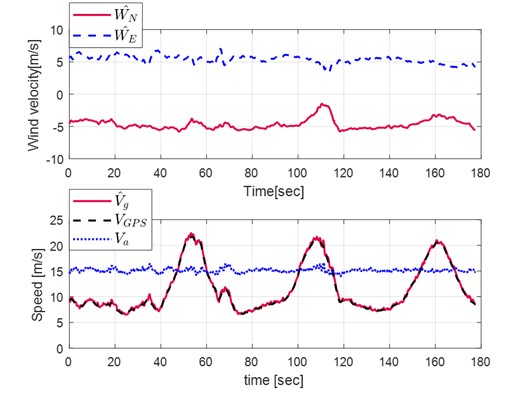
Conclusion

The experimental results show that the improved tracking performance as well as the enhanced robustness, proving the applicability of the proposed algorithm in the various mission of the fixed-wing UAV in wind disturbance environment.

Researcher

김수현(Kim Su Hyeon)
angelfive92@gmail.com